Numerical Methods and Discretization
Using numerical techniques to provide insight into complex physical problems both quickly and accurately - and seeing where those methods let us down.
Scroll ↓
General Finite Element Code
For the final project in AME 40541: Finite Element Methods (FEM), my team and I were tasked with building a general FEM code that could handle unstructured meshes, non-homogeneous natural boundary conditions, and nonlinear problems.
We were responsible for the geometry definition of simplex elements, the creation and mapping of basis functions onto elements, the defining of partial differential equations, building a basis for specific finite elements, creating functions that compute the residual and Jacobian for each element, and computing the global residual and Jacobian for the free degrees of freedom.
More information at the project can be found here.
Solving the Poisson equation over the Notre Dame logo using the finite element method with triangular elements.
Solving linear-elastic equations over a multi-material beam using the finite element method with rectangular elements.
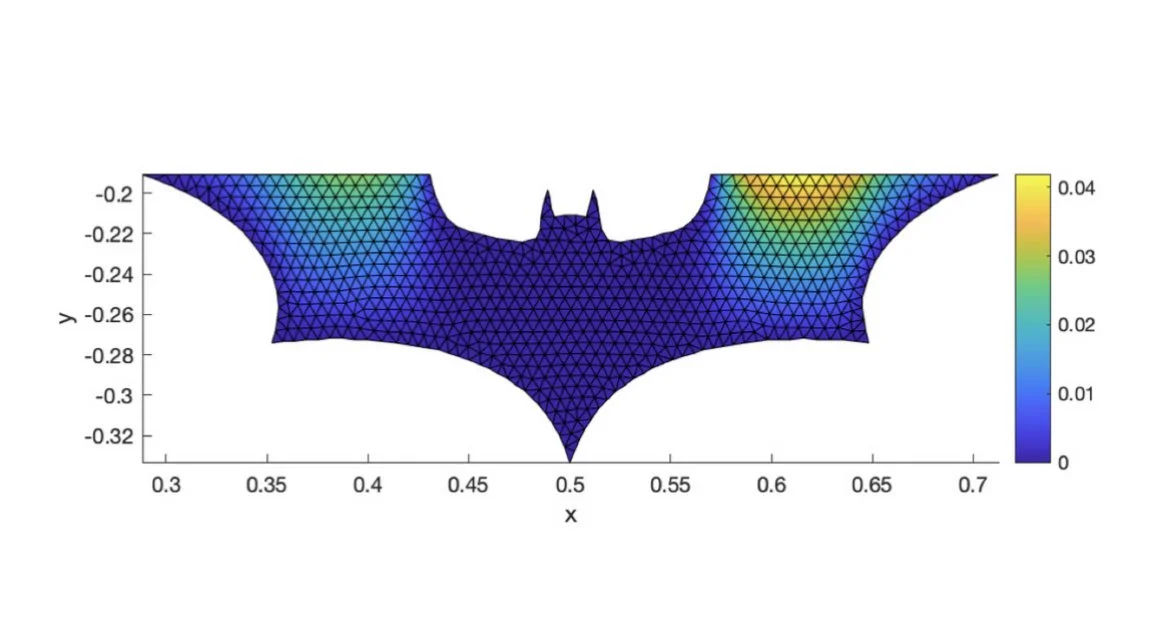
Solving a second-order linear PDE over the Batman logo using the finite element method with triangular elements.
Finite Difference Methods in Fluid Mechanics
For our final project in AME 44532: Computational Fluid Mechanics, I was tasked with solving a fluid flow problem within a rectangular cavity with moving walls using the vorticity-stream function.
I discretized the domain and used the finite-difference method to solve for the stream function, velocity, and vorticity for a variety of different conditions
More information about the project can be found here.
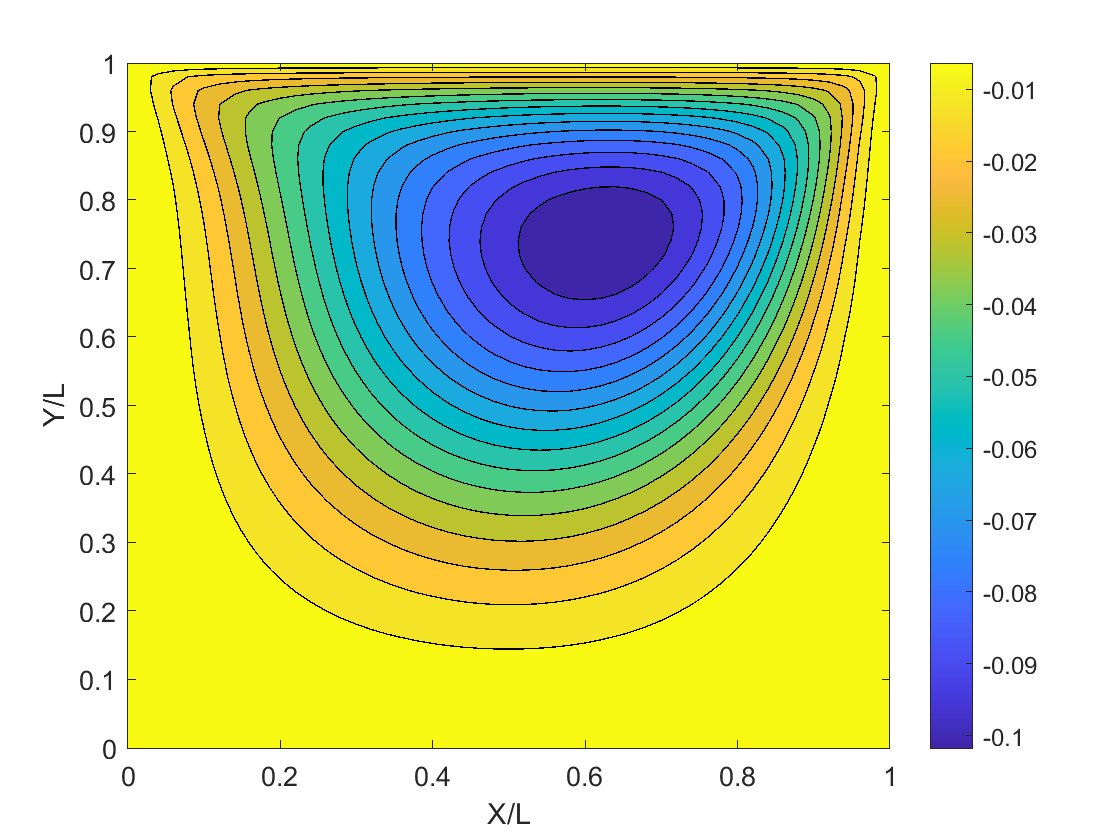
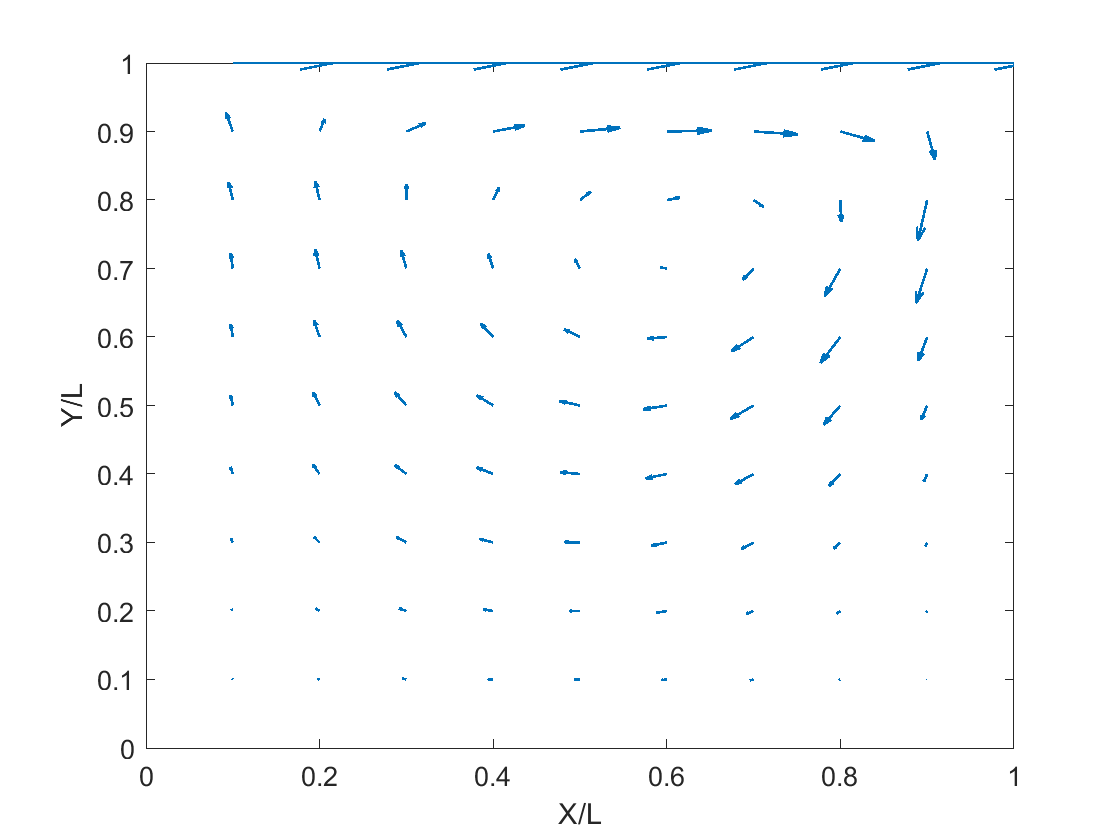
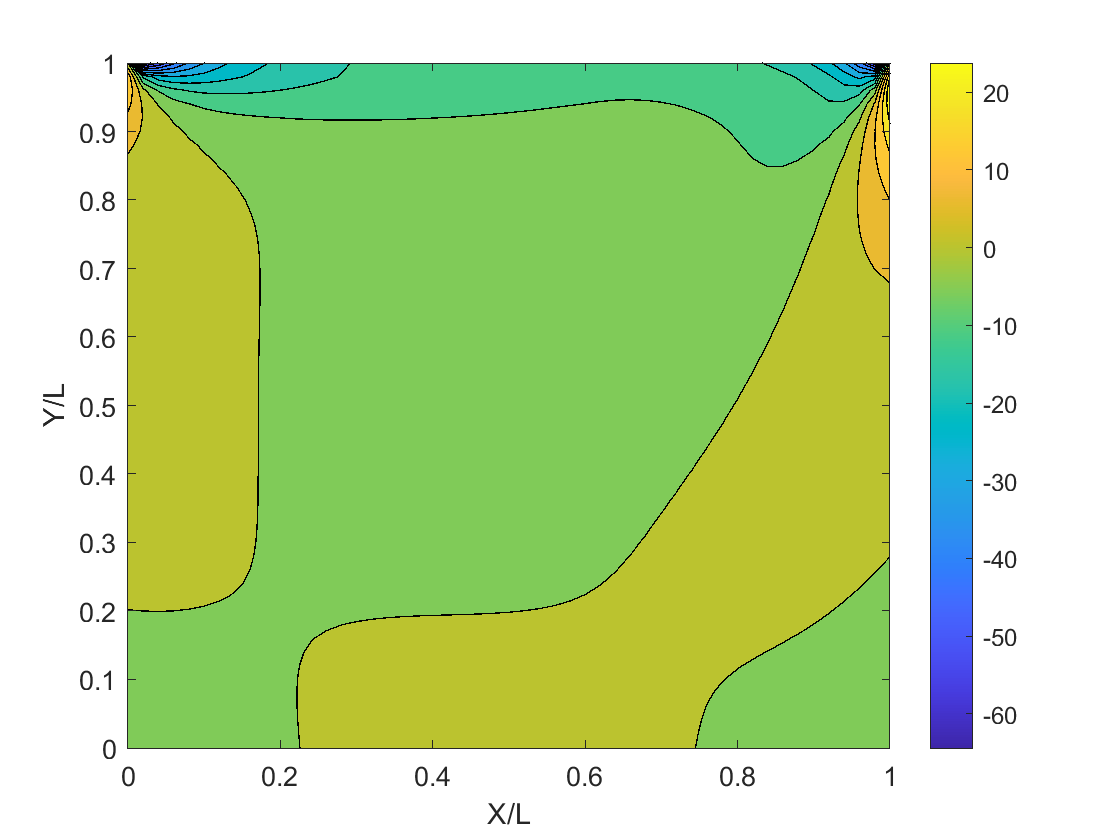
Solving vorticity-stream function for the stream function, velocity, and vorticity, respectively, using the finite-difference method.
Wave Equations
My professor in AME 30314: Differential Equations, Vibrations, and Controls gave me a variety of fun Bessel equation problems to solve and visualize in the domain of a 2D circle.
I extended the work to include off-center disturbances and multiple disturbances.
Hydrocodes and Artificial Viscosity
At my internship in the summer of 2024 at Sandia National Labs, I investigated the performance of a Sandia shock physics code, CTH, at modeling porous materials with a P-alpha porosity model.
I found oscillatory noise at shock amplitudes within an order of magnitude of the crush pressure and quantified the noise using an adapted mean squared error (MSE) formula. I further used Fast-Fourier transforms (FFT) to measure oscillatory frequency.
I reduced noise by adjusting the quadratic and linear constants associated with the artificial viscosity in CTH and confirmed noise reduction through relevant checks of the MSE and FFT amplitudes.
Me loving New Mexico outside of work.